ทฤษฎีของพีชคณิตบูลีน (Boolean algebra laws)
http://nayuki.eigenstate.org/page/boolean-algebra-laws [1]p.45boolean_algebra_laws.docx
|
ความหมาย (Notation)
False: 0 True: 1 NOT x: x x AND y: x · y x OR y: x + y x XOR y: x ⊕ y |
|
ลำดับความสำคัญ สูงไปต่ำ คือ AND, XOR, OR x + y · z หมายถึง x + (y · z) x ⊕ y · z หมายถึง x ⊕ (y · z) x + y ⊕ z หมายถึง x + (y ⊕ z) |
กฎพื้นฐาน (Basic laws)
|
Constants
NOT: 0 = 1 1 = 0 AND: 0 · 0 = 0 0 · 1 = 0 1 · 0 = 0 1 · 1 = 1 OR: 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 1 XOR: 0 ⊕ 0 = 0 0 ⊕ 1 = 1 1 ⊕ 0 = 1 1 ⊕ 1 = 0 |
|
Constant and variable
AND: 0 · x = 0 1 · x = x OR: 0 + x = x 1 + x = 1 XOR: 0 ⊕ x = x 1 ⊕ x = x |
|
One variable
NOT: NOT x = x AND: x · x = x x · x = 0 OR: x + x = x x + x = 1 XOR: x ⊕ x = 0 x ⊕ x = 1 XOR XOR สามารถเขียนได้ โดยใช้ AND, OR, NOT: x ⊕ y = (x · y) + (x · y) x ⊕ y = (x + y) · (x + y) x ⊕ y = (x + y) · (x · y) |
ทฤษฎีของพีชคณิตบูลีน (Boolean algebra laws)
|
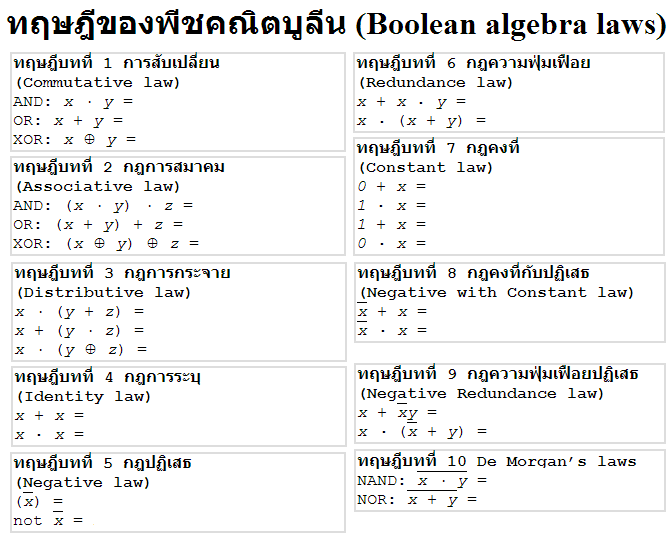
ทฤษฎีบทที่ 1 การสับเปลี่ยน (Commutative law) AND: x · y = y · x OR: x + y = y + x XOR: x ⊕ y = y ⊕ x |
|
ทฤษฎีบทที่ 2 กฎการสมาคม (Associative law) AND: (x · y) · z = x · (y · z) OR: (x + y) + z = x + (y + z) XOR: (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z) |
|
ทฤษฎีบทที่ 3 กฎการกระจาย (Distributive law) x · (y + z) = (x · y) + (x · z) x + (y · z) = (x + y) · (x + z) x · (y ⊕ z) = (x · y) ⊕ (x · z) |
|
ทฤษฎีบทที่ 4 กฎการระบุ (Identity law) x + x = x x . x = x |
|
ทฤษฎีบทที่ 5 กฎปฏิเสธ (Negative law) (x) = x not x = x |
|
ทฤษฎีบทที่ 6 กฎความฟุ่มเฟือย (Redundance law) x + x . y = x x . (x + y) = x |
|
ทฤษฎีบทที่ 7 กฎคงที่ (Constant law) 0 + x = x 1 . x = x 1 + x = 1 0 . x = 0 |
|
ทฤษฎีบทที่ 8 กฎคงที่กับปฏิเสธ (Negative with Constant law) x + x = 1 x . x = 0 |
|
ทฤษฎีบทที่ 9 กฎความฟุ่มเฟือยปฏิเสธ (Negative Redundance law) x + xy = x + y x . (x + y) = x . y |
|
ทฤษฎีบทที่ 10 De Morgan’s laws
NAND: x · y = x + y NOR: x + y = x · y |
|
กฎความฟุ่มเฟือย (Redundance law)
การดูดซับ (Absorption)
พิสูจน์ x + x · y = (x · 1) + (x · y) เพิ่ม 1 เข้าไป = x · (1 + y) ใช้ Distributivity = x · 1 = x พิสูจน์ x · (x + y) = (x + 0) · (x + y) เพิ่ม 0 เข้าไป = x + (0 · y) ใช้ Distributivity = x + 0 = x |
ไม่มีชื่อ (No name)
พิสูจน์ x + x · y = (x + x) · (x + y) = 1 · (x + y) = x + y พิสูจน์ x · (x + y) = x · x + x · y = 0 + x · y = x · y พิสูจน์ x · y + x · y = x · (y + y) = x · 1 = x พิสูจน์ (x + y) · (x + y) = x + (y · y) = x + 0 = x |